中学2年生 角度の話〈第2回〉【四街道の学習塾】
2023/11/19
こんにちは。四街道市の栗山にある学習塾、秀英ゼミナールです。
小学生、中学生、高校生対象の一斉指導・個別指導を行っています。
中学生は当塾近隣の四街道北中、千代田中のほか、旭中、四街道西中、四街道中の生徒さんが、小学生は近隣の中央小、栗山小のほか、大日小、旭小、みそら小の生徒さんが多くいます。近隣の学校以外は送迎バスを利用される生徒さんも多いです。
在籍生は四街道市が中心ですが、千葉市稲毛区、佐倉市の染井野から通塾する生徒さんもいます。
中学2年生の学習範囲、角度について学習していきましょう。
第3回の定期テスト範囲に含まれる学校も多くありますので、しっかりと覚えてくださいね。
今回は、三角形の外角と多角形の内角についてです。
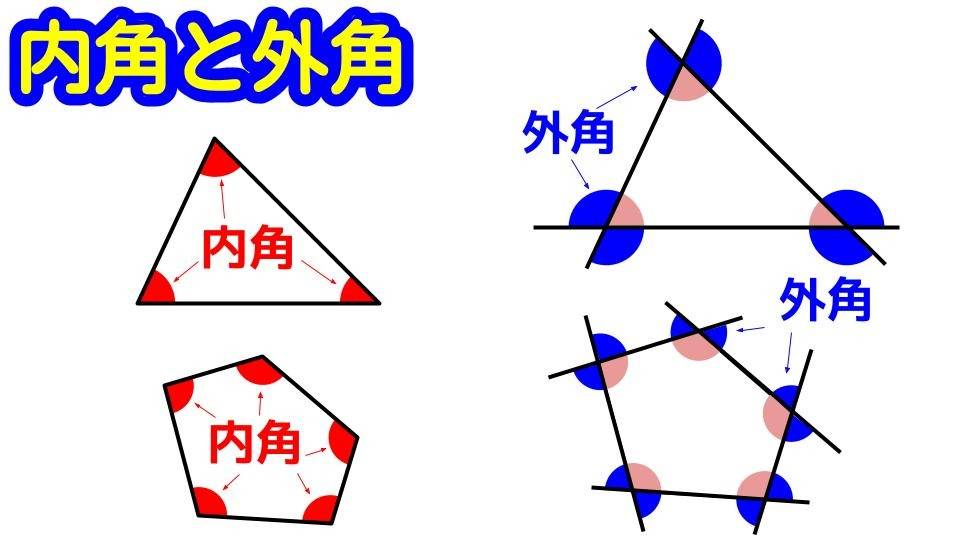
内角とは
多角形(三角形、四角形、五角形、・・・、n角形)において、図形のとなり合う2辺が作る、多角形の内側にある角のことです。
下図の、赤色の角が内角です。
外角とは
多角形において、各辺をのばしたときに、内角のとなりにある角のことです。
下図の、青色の角が外角です。
中学2年生の皆さんは、テスト前にこの決まりを覚えておいてください。
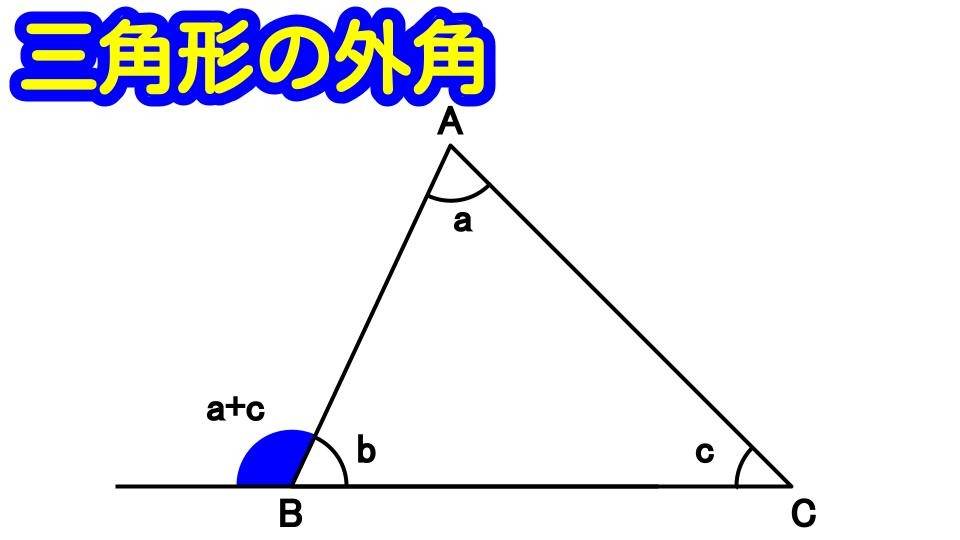
三角形の外角は、それと隣り合わない2つの内角の和に等しい
内角bの隣、青色の角が外角です。この外角は、aとcの和に等しくなります。
何故そうなるのか、2通りのやり方で考えてみましょう。
①三角形の内角bを求めてから外角を求める
三角形の内角は180度です。したがって、角bは、
180°-(a+c)
という風に求めることができます。
角bと外角を合わせると180度ですから、外角は、
180°-{180°-(a+c)}
=180°-180°+(a+c)
=a+c
となります。
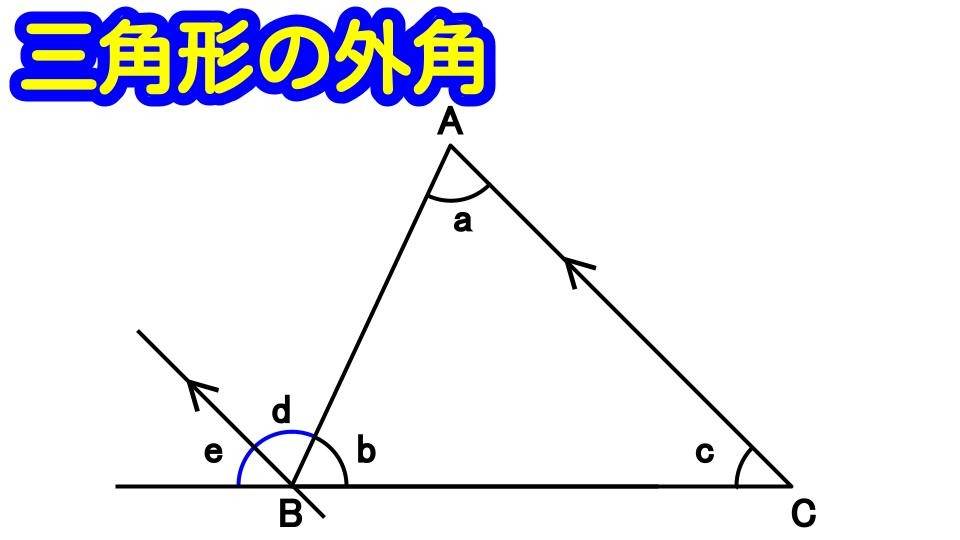
②平行線の同位角・錯角を使って求める
ACと平行で、頂点Bを通る直線をひきます。
すると、外角が2つにわかれます。角d、角eとしておきましょう。
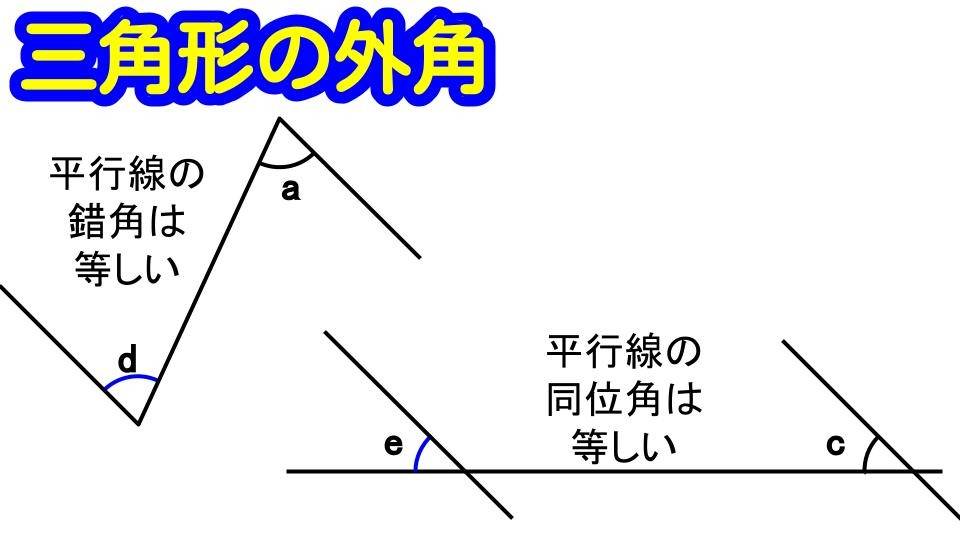
角dと角aは、平行線の錯角のため、等しくなっています。
また、角eと角cは、平行線の同位角のため、等しくなっています。
したがって、d+e=a+cとなります。
多角形の内角の和
テスト前にはこちらの公式も覚えておきましょう。
n角形の内角の和=180°×(n-2)
(五角形ならn=5、七角形ならn=7)
何故そうなるのかを考えてみましょう。
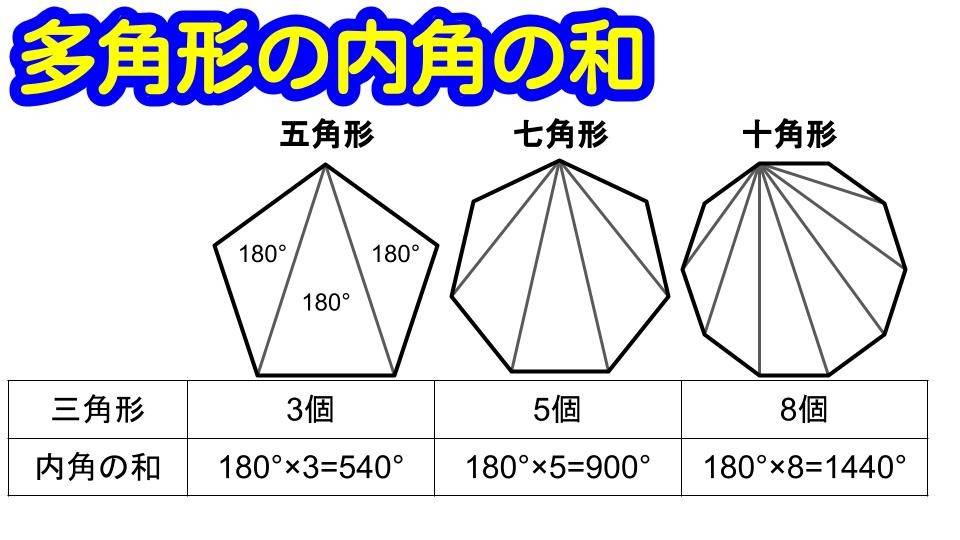
多角形の1つの頂点から対角線をひき、三角形に分けます。
三角形の数は、五角形→3個、七角形→5個、十角形→8個になりました。
それぞれの三角形の内角の和が180度なので、
五角形→180°×3=540°
七角形→180°×5=900°
十角形→180°×8=1440°
になりますね。
三角形の数は、いつも多角形の頂点の数より2つ少なくなっています。
(五角形→5-2=3個 七角形→7-2=5個 十角形→10-2=8個)
したがって、n角形の内角の和=180°×(n-2)となります。
今回は、三角形の外角と、多角形の内角の和についてでした。
テスト前にしっかり復習をして、得点源にしてくださいね。
次回は、多角形の外角について、にしようと思っています。
----------------------------------------------------------------------
秀英ゼミナール
〒284-0027
住所:千葉県 四街道市 栗山 1082-144
電話番号 :043-422-2669
小学生向けコースを四街道で展開
中学生コースを四街道で手掛ける
----------------------------------------------------------------------